9. For loops

We will now explore one of the main strengths of programming: automating repetitive tasks with loops! Here we’re going to look at a specific type of loop called a for loop, which is used when you know how many times you want to repeat an action.

Summary of commands

In Python, the general structure is like this:

for i in collection:
    do something repeatedly, where each iteration, the variable i takes on a different value in the collection

where collection is usually a list-like object of values. The for loop stops when all the items in the collection are used once. A very common expression you’ll see for collection is range(N), which is a built-in function that enumerates numbers from 0 up to N (not inclusive).

Part 1

Compute \(10!\) (ten factorial). That is, the product of all the integers from \(1\) to \(10\).

product = 1
for i in range(1, 11):    # we specify the start
    product *= i          # shorthand notation for self-multiplication
print(product)

3628800

Part 2

Compute the sum of all even numbers from \(0\) to \(100\).

Note: There are multiple ways to approach this!

• In Python, the modulo operator %, used as a % b, returns the remainder when \(a\) is divided by \(b\).

• You can change the step size in the range() function.

# using the modulo operator
running_sum = 0
for i in range(101):
    if i % 2 == 0:
        running_sum += i
print(running_sum)

# using the step parameter
running_sum2 = 0
for i in range(0, 101, 2):
    running_sum2 += i
print(running_sum2)

2550
2550

Part 3

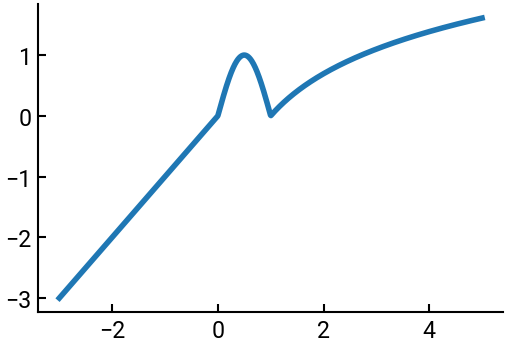
Define the following piecewise function between \(x = -3\) and \(x = 5\) using \(1000\) points and plot it.

\[\begin{split} \begin{align*} y(x) &= x \qquad &x < 0 \\ y(x) &= \sin (\pi x) \qquad &0 \le x \le 1 \\ y(x) &= \ln(x) \qquad &x > 1 \end{align*} \end{split}\]

import numpy as np
import matplotlib.pyplot as plt

# define x vector
x = np.linspace(-3, 5, 1000)

# define an empty y vector of the same length
y = np.zeros(x.shape)

# using logical indices as a mask
for i,xx in enumerate(x):    # return the index,value of each element
    if xx < 0:
        y[i] = xx
    elif xx <= 1:
        y[i] = np.sin(np.pi * xx)
    else:
        y[i] = np.log(xx)

# plot y as a function of x
fig, ax = plt.subplots()
ax.plot(x, y)
plt.show()