The tl;dr Python speedrun

The tl;dr Python speedrun#

Note

Click the and open this notebook in Colab to enable interactivity.

Note

To save your progress, make a copy of this notebook in Colab File > Save a copy and you’ll find it in My Drive > Colab Notebooks.

Part of the MATLAB tutorials in CME 100 features a condensed set of notes, which we’ve reproduced here in Python.

1. Basic operations#

(a) Using Python as a calculator#

(2 + 3) * 4 / 5

4.0

(b) Defining scalar variables#

a = 2
a

2

b = 3
b

3

c = a + b
c

5

# this is a comment
c;    # semicolon suppresses output

(c) Defining arrays and using array elements in computation#

🚨 Remember that Python is 0-indexed!

a = [1, 2, 3]
print(a)
print(a[0])
print(a[1])
print(a[2])

x = a[0] * a[1]
print(x)

[1, 2, 3]
1
2
3
2

(d) Appending arrays#

# in native Python
a = [1, 2, 3]
b = [3, 4]
c = a + b
print(c)

# in NumPy
import numpy as np
a = np.array([1, 2, 3])
b = np.array([3, 4])
c = np.concatenate([a, b])
print(c)

[1, 2, 3, 3, 4]

[1 2 3 3 4]

2. Plotting#

(a) Basic plotting#

import numpy as np
import matplotlib.pyplot as plt

x = np.arange(0, 15, 0.1)
y = np.sin(x) * x

fig, ax = plt.subplots()
ax.plot(x, y)
ax.set(xlabel="Time", ylabel="Position", title="Pretty plot")
plt.show()
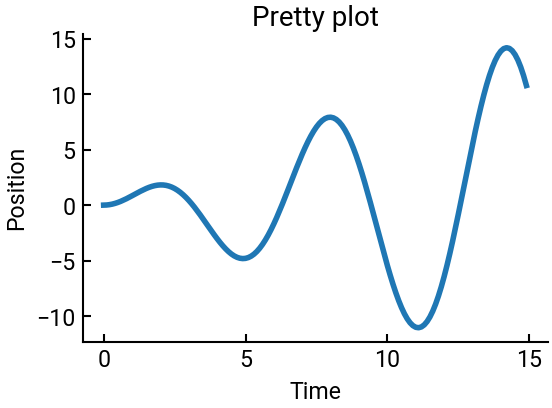
../_images/ac32a21ffe871aa17da1001cdbd6d64a758d44a841de4a7987a2f0155b975bee.png

We can easily plot multiple datasets on a single set of axes.

z = np.cos(x) * x ** 0.5

fig, ax = plt.subplots()
ax.plot(x, y)
ax.plot(x, z, ls='--')
ax.set(xlabel="Time", ylabel="Position", title="Pretty plots")
plt.show()
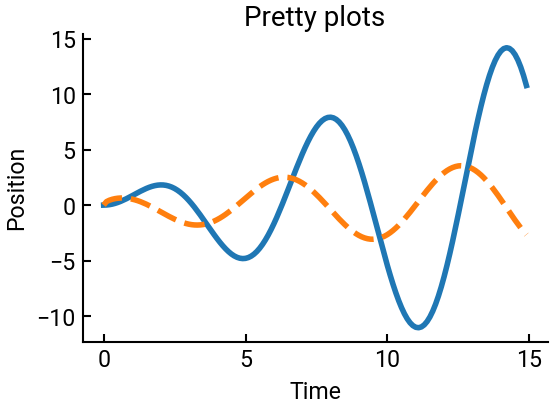
../_images/c1efedba238274063a058bdca684d48beb230920e7fc189945175e454b29aa5e.png

Or we can put them on separate axes on the same figure.

fig, ax = plt.subplots(figsize=(10,8), nrows=2, ncols=2)
ax[0,0].plot(x, y)
ax[0,1].plot(x, z, ls='--')
ax[1,0].plot(y, z, ls=':')
plt.show()
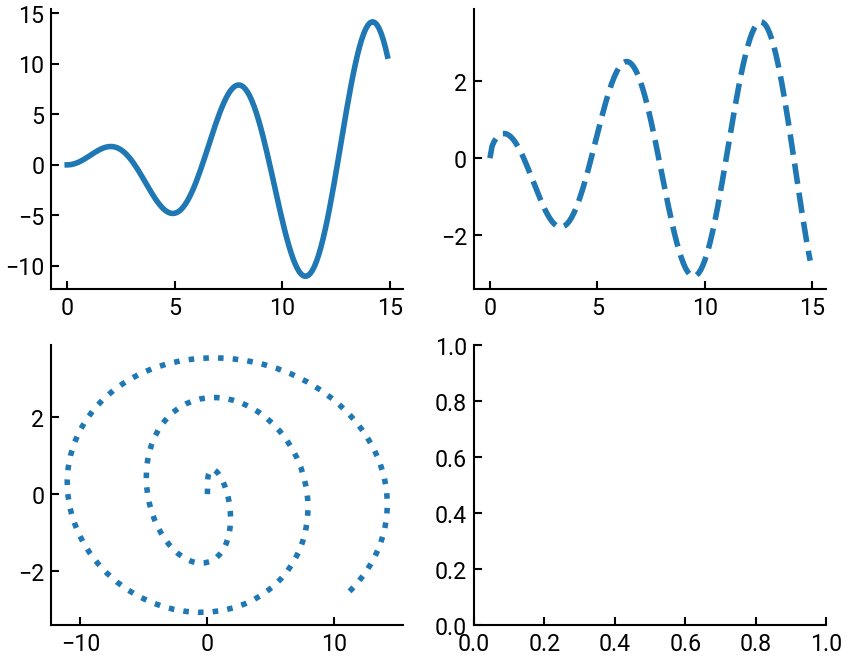
../_images/3bd37d1c4e9e93ff7c120da31ad60326ca7995d8bdeb3d3e433819c0de593026.png

3. Plotting in 3D#

(a) Parametric curves#

import numpy as np
import matplotlib.pyplot as plt

t = np.arange(0, 4*np.pi, 0.1)
x = np.cos(t)
y = np.sin(t)
z = t

fig = plt.figure(figsize=(6,6))
ax = fig.add_subplot(projection='3d')
ax.plot(x, y, z)
plt.show()
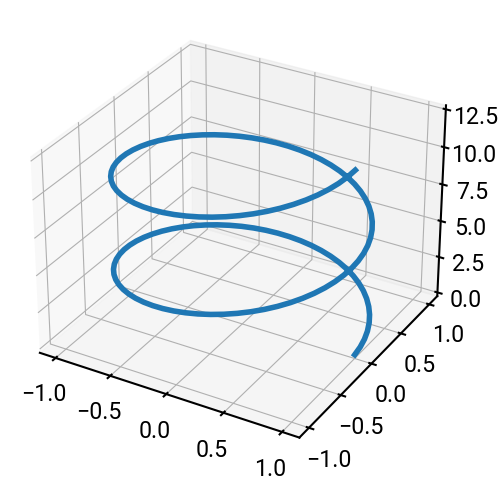
../_images/4ce5ad1bf02fce475fdcf891802ee55be25df3221422c6bc5a8cbab569ec2c76.png

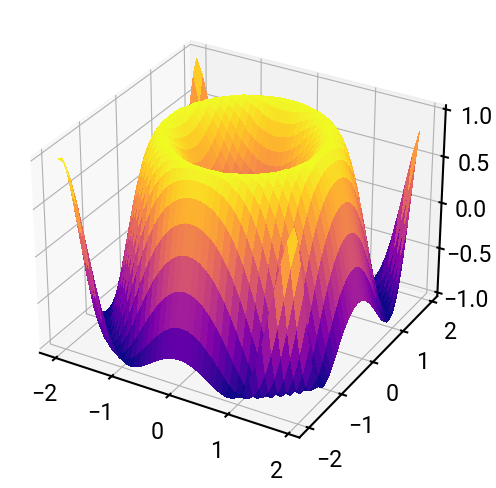
(b) Surfaces#

import numpy as np
X, Y = np.meshgrid(np.arange(-2, 2, 0.1), np.arange(-2, 2, 0.1))
Z = np.sin(X ** 2 + Y ** 2)

fig = plt.figure(figsize=(6,6))
ax = fig.add_subplot(projection='3d')
ax.plot_surface(X, Y, Z, cmap='plasma', antialiased=False)
plt.show()
../_images/f66ba6c044749bd00636052c2d3a6f17ff91a3814d37d59737db3b9998ade236.png

4. Creating a simple script#

PASS

5. Creating a function#

def dot_product(a, b):
    return a[0] * b[0] + a[1] * b[1] + a[2] * b[2]

a = [1, 2, 3]
b = [2, 3, 4]
dot_product(a, b)

20

6. Using functions#

Where we use the function from the previous cell.

import numpy as np
a = [1, 2, 3]
b = [2, 3, 4]
c = dot_product(a, b)
proj_ab = c / np.linalg.norm(b)
print(c, proj_ab)

20 3.7139067635410377

7. Programming in Python#

def factorial_for(n):
    product = 1
    for i in range(2, n+1):
        product *= i
    return product

def factorial_while(n):
    product = 1
    i = 1
    while i <= n:
        product *= i
        i += 1
    return product

def factorial_if(n):
    product = 1
    i = 1
    while True:
        product *= i
        i += 1
        if i > n:
            break
    return product

print(factorial_for(8), factorial_while(8), factorial_if(8))

40320 40320 40320

Conclusion#

Congrats on making it to the end of this accelerated tutorial!

Contents