13. Newton’s method example

Here is another engineering application using Newton’s method applied to a diode.

A diode is a semiconductor component whose property is its tendency to conduct electric current in one direction only. When the voltage reaches a threshold value (typically around \(700\) mV), the diode conducts current in the forward direction.

The current-voltage (\(I-V\)) characteristic of the diode used in this exmple is given by:

\[ I_{\mathrm{diode}} = I_{\mathrm{s}} \left( e^{\dfrac{q V_{\mathrm{diode}}}{k_{\mathrm{B}}T}} - 1 \right) \]

where \(I_{\mathrm{s}} = 0.07\,\text{pA} = 7 \times 10^{-14}\,\text{A}\) and \(\dfrac{k_{\mathrm{B}}T}{q} = 26\,\text{mA}\) at \(300\,\text{K}\).

Compute the current in the following circuit:

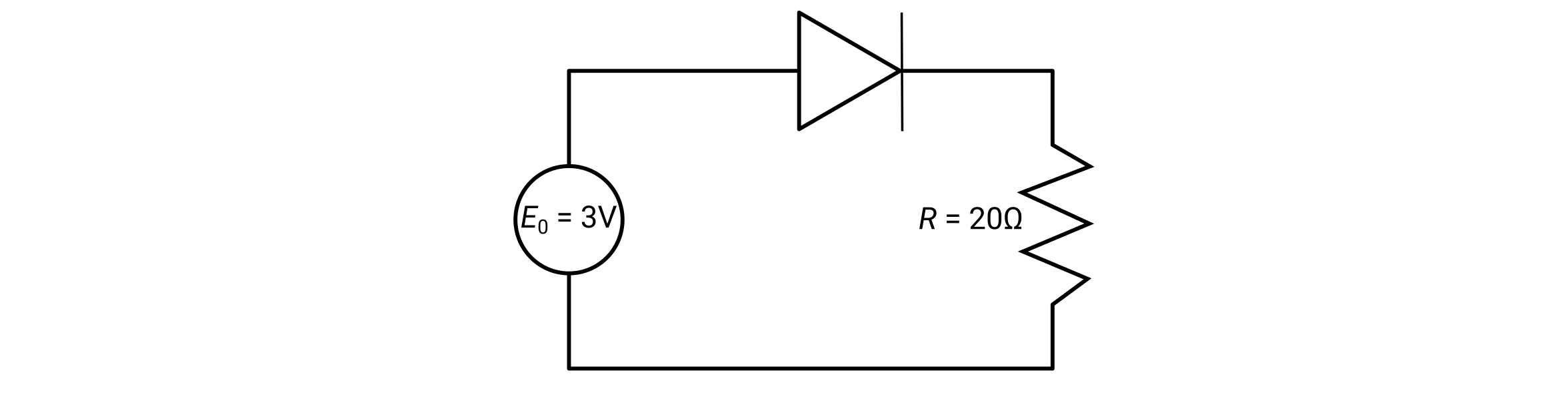
We know from Kirchhoff’s voltage law: \(E_0 = V_{\mathrm{diode}} + IR\)

We can substitute the current \(I\) by its expression as a function of \(V_{\mathrm{diode}}\) using the given \(I-V\) characteristic:

\[ E_0 = V_{\mathrm{diode}} + R I_{\mathrm{s}} \left( e^{\dfrac{q V_{\mathrm{diode}}}{k_{\mathrm{B}}T}} - 1 \right) \]

or

\[ E_0 - V_{\mathrm{diode}} - R I_{\mathrm{s}} \left( e^{\dfrac{q V_{\mathrm{diode}}}{k_{\mathrm{B}}T}} - 1 \right) = 0\]

This gives us an equation for \(V_{\mathrm{diode}}\) of the form \(f(V_{\mathrm{diode}}) = 0\), which can be solved using Newton’s method. The current is then obtained using the diode \(I-V\) characteristic as a function of \(V_{\mathrm{diode}}\).

The algorithm for Newton’s method has only a few steps: Starting from an initial guess \(V_0\), a better approximation of \(V\) is obtained from the following expression:

\[ V_1 = V_0 - \dfrac{f(V_0)}{f'(V_0)} \]

where \(f'(V_0)\) is the derivative of \(f()\) evaluated at \(V_0\). Or, more generally, the iterative algorithm is:

\[ V_{n+1} = V_n - \dfrac{f(V_n)}{f'(V_n)} \]

In our case, the derivative of \(f\) follows from a straightforward power rule and chain rule:

\[ f'(V) = -1 - RI_{\mathrm{s}} \dfrac{q}{k_{\mathrm{B}}T} e^{\dfrac{q V}{k_{\mathrm{B}}T}} \]

Perform several iterations of Newton’s method using the for loop. Find the diode voltage and the current in the circuit using \(20\) iterations.

import numpy as np
import matplotlib.pyplot as plt

# constants
E0 = 3
Is = 7e-14
R = 200
C = 0.026    # kT/q

Vd = 1   # init guess

for i in range(20):
    fp = -1 - Is * R / C * np.exp(Vd / C)
    f = E0 - Vd - Is * R * (np.exp(Vd / C) - 1)
    Vd = Vd - f / fp

I = Is * (np.exp(Vd / C) - 1)
print(f"The diode voltage is {Vd:.4f} V and the current is {I:.4f} A.")

The diode voltage is 0.6718 V and the current is 0.0116 A.