10. While loops

Now that we’ve covered for loops, it’s time to talk about its sister construct—while loops. The while loop is used when you know the stop condition, but might not know or don’t care how long it takes to get there.

Summary of commands

In Python, the general structure is like this:

while condition:
    <do something repeatedly until condition becomes False>
    # Try not to get stuck in an infinite loop!

We’ll also see the following commands:

• np.absolute(x) - returns the absolute value of \(x\)

• np.sqrt(x) - returns the square root of \(x\).

• list.append(x) - adds the element x to the end of an existing list object. (not NumPy array!)

So which loop should I use?

Your choice should be based on your stop condition: Do you have a fixed number of iterations, or do you have a fixed criteria? Often, the same problem can be solved using either construct (you’ll find that the body of the loop remains largely identical), one will just be more efficient than the other, not to mention more logical when a human is reading the code.

Approximating square roots

If \(x\) is an approximate value of the square root of a number \(a\), then

\[ x' = \dfrac{1}{2} \left( x + \dfrac{a}{x} \right) \]

is generally a better approximation. For example, with \(a = 2\), starting with \(x = 1\), we obtain the following successive approximations: \(1, \dfrac{3}{2}, \dfrac{17}{12}, \dfrac{577}{408}, \dots\) approaching in the limit the true value of \(\sqrt{2} = 1.4142135...\)

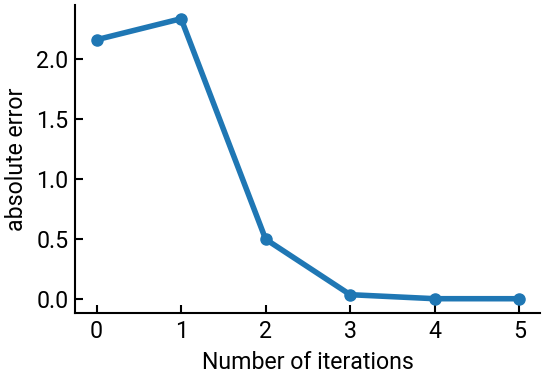
Using the above formula, write a script to compute iteratively the value of \(\sqrt{10}\). At each step, compare your solution to the exact value of \(\sqrt{10}\) and stop your iteration when the difference between your solution and the exact one is less than \(10^{-4}\). Start the iteration with the initial guess \(x = 1\). Plot the absolute value of the error versus the current iteration number.

import numpy as np
import matplotlib.pyplot as plt

a = 10
x = [1]   # we will keep x as a list to make it easy to grow
thresh = 1e-4

while np.absolute(x[-1] - np.sqrt(a)) >= thresh:
    # a slick way to always query the last element of x
    x.append(1/2 * (x[-1] + a / x[-1]))

print(f"Numerical solution: {x[-1]}")
print(f"Exact solution: {np.sqrt(a)}")

fig, ax = plt.subplots()
ax.plot(np.absolute(x - np.sqrt(a)), 'o-')
ax.set(xlabel="Number of iterations", ylabel="absolute error")
plt.show()

Numerical solution: 3.162277665175675
Exact solution: 3.1622776601683795

Note

In MATLAB, it’s easy to create an array that continually grows longer as you add more elements to it in a loop. This feature is called dynamic resizing and while it is fine, it is generally recommended to avoid doing so as it eats up a lot of memory and is inefficient. It could also be dangerous: If you don’t know the size ahead of time, what if your vector grows infinitely long? ☠️

In fact, Python NumPy arrays cannot change in size once created and you have to preallocate arrays properly for your problem. In the above, we used a regular list data structure which is efficient to grow using append().