Contents

Featurization notebook

Authors: Enze Chen and Mark Asta (University of California, Berkeley)

Note

This is an interactive exercise, so you will want to click the and open the notebook in DataHub (or Colab for non-UCB students).

Learning objectives

This notebook discuss featurization and how we can apply our domain knowledge to create physically-meaningful features for ML applications. By the end of this notebook, you will be able to:

  1. Articulate why it’s important to use physically-meaningful features for MI.

  2. Use the matminer package to featurize chemical formulas.

We will progress through most of this exercise together as a group, and if there’s a part that’s particularly tricky, please do take time to review it. As always, we’re happy to hear from you if you have any questions.

Contents

These exercises are grouped into the following sections:

  1. Overview

  2. matminer

  3. Model complexity

  4. Feature selection

Overview

Back to top

From our live discussion, we learned that creating physically-meaningful features will improve interpretability of our models as well as their predictive performance. This is especially true when we have small and sparse datasets, which tends to be the case for MI applications. With the right choice of typically a few features, we might be able to uncover a strong correlation with the target property of interest and simplify our modeling problem.

So far, we’ve been working with materials datasets and building ML models that already do this, so this idea may not be too surprising to you. For example, it is because we know that the atomic number is correlated with atomic weight that we might choose to use atomic number as a feature to predict the atomic weight, and it turned out to give good performance, even with a simple model like linear regression. If someone did not know this information, they could use many more features and still fail to get a good ML model. We will now show this is the case.

First import everything because we’re getting lazy

Although, fwiw, if you are sharing notebooks with others, it’s not a bad idea to import everything at the top. That way, if a user does not have a package, they find out right away and can go install it rather than discovering this midway through and having to interrupt their flow. 🌊

import numpy as np
import pandas as pd
pd.set_option('display.max_columns', None)
pd.set_option('display.max_rows', 300)
import matplotlib.pyplot as plt
%matplotlib inline

from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, mean_absolute_error
from sklearn.model_selection import KFold, cross_val_score, cross_val_predict

plt.rcParams.update({'figure.figsize':(8,6),       # Increase figure size
                     'font.size':20,               # Increase font size
                     'mathtext.fontset':'cm',      # Change math font to Computer Modern
                     'mathtext.rm':'serif',        # Documentation recommended follow-up
                     'lines.linewidth':5,          # Thicker plot lines
                     'lines.markersize':12,        # Larger plot points
                     'axes.linewidth':2,           # Thicker axes lines (but not too thick)
                     'xtick.major.size':8,         # Make the x-ticks longer (our plot is larger!)
                     'xtick.major.width':2,        # Make the x-ticks wider
                     'ytick.major.size':8,         # Ditto for y-ticks
                     'ytick.major.width':2,        # Ditto for y-ticks
                     'xtick.direction':'in', 
                     'ytick.direction':'in'})

Choosing bad features

Now we’ll choose a few features that are the column names of our elemental properties DataFrame and we’ll store these features into a features list. We then load in the DataFrame, making sure to drop any rows that have NaN in those columns (df.dropna(subset=features)) so that we can actually perform linear regression. Feel free to add more features to the list, just don’t add atomic_number!

features = ['row', 'electronegativity', 'molar_volume']
df = pd.read_csv('../../assets/data/week_1/04/elem_props.csv')
df = df.dropna(subset=features)
print(f'There are {len(df)} rows of the data remaining.')
display(df.head())

X = df[features]
# X = df[['atomic_number']]    # uncomment this line and see what happens!
y = df['atomic_mass']

scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

lr = LinearRegression()
kfold = KFold(n_splits=5, shuffle=True)
scores = cross_val_score(lr, X_scaled, y, scoring='neg_root_mean_squared_error', cv=kfold)
print(f'The average CV score is {-np.mean(scores):.3f}.')

lr.fit(X_scaled, y)
yhat = lr.predict(X_scaled)
print(f'The slopes are {lr.coef_} and the intercept term is {lr.intercept_}')

fig, ax = plt.subplots(figsize=(7,7))
ax.scatter(y, yhat, s=40)
yhat = cross_val_predict(lr, X_scaled, y, cv=kfold)
ax.plot(y, y, c='k', zorder=-5)
ax.set_xlabel('actual atomic weight')
ax.set_ylabel('predicted atomic weight')
ax.set_aspect('equal')
plt.show()

There are 94 rows of the data remaining.
symbol name atomic_number atomic_mass atomic_radius row group is_metal electronegativity density_solid melting_point molar_volume refractive_index elec_resist therm_cond youngs_mod poissons_ratio
0 H Hydrogen 1 1.007940 0.25 1 1 False 2.20 NaN 14.01 K 11.42 1.000132 (gas; liquid 1.12)(no units) NaN 0.1805 NaN NaN
2 Li Lithium 3 6.941000 1.45 2 1 True 0.98 535.0 453.69 K 13.02 NaN 9.500000e-08 85.0000 4.9 NaN
3 Be Beryllium 4 9.012182 1.05 2 2 True 1.57 1848.0 1560.0 K 4.85 NaN 3.800000e-08 190.0000 287.0 0.032
4 B Boron 5 10.811000 0.85 2 13 False 2.04 2460.0 2349.0 K 4.39 NaN 1.000000e+12 27.0000 NaN NaN
5 C Carbon 6 12.010700 0.70 2 14 False 2.55 2267.0 3800.0 K 5.29 2.417 (diamond)(no units) 1.000000e-05 140.0000 NaN NaN 
The average CV score is 29.180.
The slopes are [74.49875132 18.53037859  3.99969981] and the intercept term is 122.69665529765962
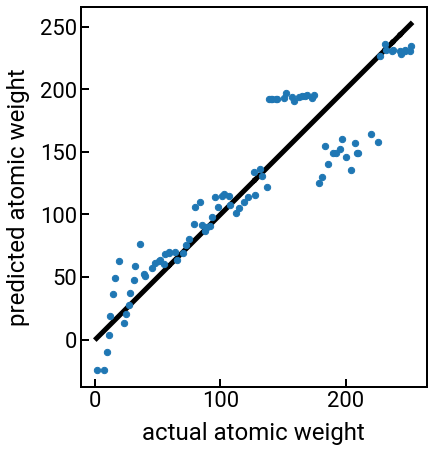
../../_images/features_blank_5_3.png

Pause and reflect: Note how we can use many more features to build our ML model and still create the parity plot the same way as before, since it only depends on the output predictions. Based on the parity plot and coefficients, can you tell how your choice of features are being leveraged for the prediction?

What you should observe is that using any combination of the other provided features basically sucks for predicting the atomic weight, and as soon as we switch to atomic number, everything is right with the world. 😇 This is encouraging, but we know that in the real world, materials properties won’t be this strongly dependent on each other, and then it becomes very unclear which features we should choose. Also, features won’t always be given to you in a nice data table like the previous example, so is there a way we can programmatically and automatically generate some physically-meaningful features from a material’s chemical formula or crystal structure?

matminer

Back to top

matminer

It turns out that there are now many Python packages that are able to generate features, and because we’re proud Berkeley Bears, we will use the matminer package developed by scientists at UCB and LBL. This package is actually quite popular as a general purpose featurization tool, and it will not only be great for teaching featurizations, but we also hope you will use it in your self-directed research projects. One notable feature of matminer is that it mostly uses pandas DataFrames as inputs and outputs, which is great news for us!

As a quick aside, we wanted to wait until now to mention that matminer also has datasets and database retrieval objects that are pretty cool to look into if you want to explore more data mining on your own. We won’t spend too much time discussing these tools, though we will utilize one below.

Featurizing a chemical formula

The first thing we can try is to take a chemical formula and enumerate a set of properties based on the formula. This is appealing because chemical formulas seem like a fairly accessible property of the material (otherwise what did you even make??) and chemistry determines a lot of properties, so we’d like to leverage it.

To featurize a chemical formula that is represented as a string, we have to first convert it into a Pymatgen Composition object, which allows us to make sense of the elements present, subscripts, etc. As you can imagine, matminer builds off of the functionality in Pymatgen. 😉 To perform the actual conversion, we use the StrToComposition class from the matminer.featurizers.conversions submodule, and this is called as follows:

from matminer.featurizers.conversions import StrToComposition
str_comp = StrToComposition(target_col_id='composition')
data = str_comp.featurize_dataframe(data, col_id='formula')

where:

  1. The first line is the package import statement.

  2. The second line constructs the conversion object, and specifies that the new column holding the Composition will be named 'composition'.

  3. The third line performs the conversion (using featurize_dataframe(df, col_id) and stores the output in a new DataFrame. The col_id parameter says that the name of the existing column that holds the chemical formulas is named 'formula'.

Band gap data

from matminer.datasets import load_dataset
bg_data = load_dataset('matbench_expt_gap')
bg_data = bg_data[bg_data['gap expt'] > 0].reset_index(drop=True)   # just look at positive band gaps, trims dataset
display(bg_data.head())                      # pretty straightforward!

from matminer.featurizers.conversions import StrToComposition
str_to_comp = StrToComposition(target_col_id='composition_pmg')
bg_data_comp = str_to_comp.featurize_dataframe(bg_data, col_id='composition')
display(bg_data_comp.head())
composition gap expt
0 Ag0.5Ge1Pb1.75S4 1.83
1 Ag0.5Ge1Pb1.75Se4 1.51
2 Ag2GeS3 1.98
3 Ag2GeSe3 0.90
4 Ag2HgI4 2.47
composition gap expt composition_pmg
0 Ag0.5Ge1Pb1.75S4 1.83 (Ag, Ge, Pb, S)
1 Ag0.5Ge1Pb1.75Se4 1.51 (Ag, Ge, Pb, Se)
2 Ag2GeS3 1.98 (Ag, Ge, S)
3 Ag2GeSe3 0.90 (Ag, Ge, Se)
4 Ag2HgI4 2.47 (Ag, Hg, I)

Enumerating elemental properties

Magpie features

Once we have a column of Composition objects, we’re ready to perform the featurization! We will use one of the featurizers from the matminer.featurizers.composition submodule, namely ElementProperty (although there are many, many more). For the ElementProperty, we will demonstrate the featurizer.from_preset('magpie') class method, which creates an object that can automatically engineer 132 new features based on the method by Ward et al. npj Comput. Mater., 2016. 🤯

It does this by first calculating what the property (e.g., electronegativity) is for each element in the composition. It then computes a set of statistical quantities based on the set of elemental properties for each composition, such as the mean, minimum, maximum, etc. These statistical quantities of the elemental properties then become the new features for that material.

The ElementProperty object can then call the featurize_dataframe(df, col_id='comp_col_name') method to generate all the columns with features.

from matminer.featurizers.composition import ElementProperty
featurizer = ElementProperty.from_preset('magpie')
bg_data_featurized = featurizer.featurize_dataframe(bg_data_comp, col_id='composition_pmg')
y = bg_data_featurized['gap expt']
bg_data_featurized.head()
composition gap expt composition_pmg MagpieData minimum Number MagpieData maximum Number MagpieData range Number MagpieData mean Number MagpieData avg_dev Number MagpieData mode Number MagpieData minimum MendeleevNumber MagpieData maximum MendeleevNumber MagpieData range MendeleevNumber MagpieData mean MendeleevNumber MagpieData avg_dev MendeleevNumber MagpieData mode MendeleevNumber MagpieData minimum AtomicWeight MagpieData maximum AtomicWeight MagpieData range AtomicWeight MagpieData mean AtomicWeight MagpieData avg_dev AtomicWeight MagpieData mode AtomicWeight MagpieData minimum MeltingT MagpieData maximum MeltingT MagpieData range MeltingT MagpieData mean MeltingT MagpieData avg_dev MeltingT MagpieData mode MeltingT MagpieData minimum Column MagpieData maximum Column MagpieData range Column MagpieData mean Column MagpieData avg_dev Column MagpieData mode Column MagpieData minimum Row MagpieData maximum Row MagpieData range Row MagpieData mean Row MagpieData avg_dev Row MagpieData mode Row MagpieData minimum CovalentRadius MagpieData maximum CovalentRadius MagpieData range CovalentRadius MagpieData mean CovalentRadius MagpieData avg_dev CovalentRadius MagpieData mode CovalentRadius MagpieData minimum Electronegativity MagpieData maximum Electronegativity MagpieData range Electronegativity MagpieData mean Electronegativity MagpieData avg_dev Electronegativity MagpieData mode Electronegativity MagpieData minimum NsValence MagpieData maximum NsValence MagpieData range NsValence MagpieData mean NsValence MagpieData avg_dev NsValence MagpieData mode NsValence MagpieData minimum NpValence MagpieData maximum NpValence MagpieData range NpValence MagpieData mean NpValence MagpieData avg_dev NpValence MagpieData mode NpValence MagpieData minimum NdValence MagpieData maximum NdValence MagpieData range NdValence MagpieData mean NdValence MagpieData avg_dev NdValence MagpieData mode NdValence MagpieData minimum NfValence MagpieData maximum NfValence MagpieData range NfValence MagpieData mean NfValence MagpieData avg_dev NfValence MagpieData mode NfValence MagpieData minimum NValence MagpieData maximum NValence MagpieData range NValence MagpieData mean NValence MagpieData avg_dev NValence MagpieData mode NValence MagpieData minimum NsUnfilled MagpieData maximum NsUnfilled MagpieData range NsUnfilled MagpieData mean NsUnfilled MagpieData avg_dev NsUnfilled MagpieData mode NsUnfilled MagpieData minimum NpUnfilled MagpieData maximum NpUnfilled MagpieData range NpUnfilled MagpieData mean NpUnfilled MagpieData avg_dev NpUnfilled MagpieData mode NpUnfilled MagpieData minimum NdUnfilled MagpieData maximum NdUnfilled MagpieData range NdUnfilled MagpieData mean NdUnfilled MagpieData avg_dev NdUnfilled MagpieData mode NdUnfilled MagpieData minimum NfUnfilled MagpieData maximum NfUnfilled MagpieData range NfUnfilled MagpieData mean NfUnfilled MagpieData avg_dev NfUnfilled MagpieData mode NfUnfilled MagpieData minimum NUnfilled MagpieData maximum NUnfilled MagpieData range NUnfilled MagpieData mean NUnfilled MagpieData avg_dev NUnfilled MagpieData mode NUnfilled MagpieData minimum GSvolume_pa MagpieData maximum GSvolume_pa MagpieData range GSvolume_pa MagpieData mean GSvolume_pa MagpieData avg_dev GSvolume_pa MagpieData mode GSvolume_pa MagpieData minimum GSbandgap MagpieData maximum GSbandgap MagpieData range GSbandgap MagpieData mean GSbandgap MagpieData avg_dev GSbandgap MagpieData mode GSbandgap MagpieData minimum GSmagmom MagpieData maximum GSmagmom MagpieData range GSmagmom MagpieData mean GSmagmom MagpieData avg_dev GSmagmom MagpieData mode GSmagmom MagpieData minimum SpaceGroupNumber MagpieData maximum SpaceGroupNumber MagpieData range SpaceGroupNumber MagpieData mean SpaceGroupNumber MagpieData avg_dev SpaceGroupNumber MagpieData mode SpaceGroupNumber
0 Ag0.5Ge1Pb1.75S4 1.83 (Ag, Ge, Pb, S) 16.0 82.0 66.0 36.275862 23.552913 16.0 65.0 88.0 23.0 83.482759 4.984542 88.0 32.0650 207.2000 175.1350 85.163324 62.045964 32.06500 388.36 1234.93 846.57 611.499655 251.480143 388.36 11.0 16.0 5.0 14.896552 1.217598 16.0 3.0 6.0 3.0 4.000000 1.103448 3.0 105.0 146.0 41.0 119.724138 16.247325 105.0 1.93 2.58 0.65 2.396207 0.202806 2.58 1.0 2.0 1.0 1.931034 0.128419 2.0 0.0 4.0 4.0 2.965517 1.141498 4.0 0.0 10.0 10.0 4.482759 4.946492 0.0 0.0 14.0 14.0 3.37931 5.127229 0.0 6.0 28.0 22.0 12.758621 7.700357 6.0 0.0 1.0 1.0 0.068966 0.128419 0.0 0.0 4.0 4.0 2.620690 1.046373 2.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 4.0 3.0 2.689655 0.994055 2.0 16.33 28.110000 11.780000 25.311724 1.875196 25.786875 0.0 2.202 2.202 1.267724 1.030925 2.202 0.0 0.0 0.0 0.0 0.0 0.0 70.0 225.0 155.0 139.482759 76.670630 70.0
1 Ag0.5Ge1Pb1.75Se4 1.51 (Ag, Ge, Pb, Se) 32.0 82.0 50.0 46.206897 17.388823 34.0 65.0 89.0 24.0 84.034483 5.479191 89.0 72.6400 207.2000 134.5600 111.036428 46.423794 78.96000 494.00 1234.93 740.93 669.783793 227.362568 494.00 11.0 16.0 5.0 14.896552 1.217598 16.0 4.0 6.0 2.0 4.551724 0.760999 4.0 120.0 146.0 26.0 128.000000 11.034483 120.0 1.93 2.55 0.62 2.379655 0.187967 2.55 1.0 2.0 1.0 1.931034 0.128419 2.0 0.0 4.0 4.0 2.965517 1.141498 4.0 10.0 10.0 0.0 10.000000 0.000000 10.0 0.0 14.0 14.0 3.37931 5.127229 0.0 11.0 28.0 17.0 18.275862 4.694411 16.0 0.0 1.0 1.0 0.068966 0.128419 0.0 0.0 4.0 4.0 2.620690 1.046373 2.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 4.0 3.0 2.689655 0.994055 2.0 16.33 28.110000 11.780000 25.385172 1.905589 25.920000 0.0 0.799 0.799 0.493655 0.336932 0.799 0.0 0.0 0.0 0.0 0.0 0.0 14.0 225.0 211.0 108.586207 104.370987 14.0
2 Ag2GeS3 1.98 (Ag, Ge, S) 16.0 47.0 31.0 29.000000 13.000000 16.0 65.0 88.0 23.0 78.833333 9.222222 88.0 32.0650 107.8682 75.8032 64.095233 32.030233 32.06500 388.36 1234.93 846.57 807.723333 419.363333 388.36 11.0 16.0 5.0 14.000000 2.000000 16.0 3.0 5.0 2.0 3.833333 0.833333 3.0 105.0 145.0 40.0 120.833333 16.111111 105.0 1.93 2.58 0.65 2.268333 0.311667 2.58 1.0 2.0 1.0 1.666667 0.444444 2.0 0.0 4.0 4.0 2.333333 1.666667 4.0 0.0 10.0 10.0 5.000000 5.000000 0.0 0.0 0.0 0.0 0.00000 0.000000 0.0 6.0 14.0 8.0 9.000000 3.000000 6.0 0.0 1.0 1.0 0.333333 0.444444 0.0 0.0 4.0 4.0 1.666667 1.111111 2.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 4.0 3.0 2.000000 0.666667 2.0 16.33 25.786875 9.456875 22.170937 3.893958 25.786875 0.0 2.202 2.202 1.164833 1.037167 2.202 0.0 0.0 0.0 0.0 0.0 0.0 70.0 225.0 155.0 147.500000 77.500000 70.0
3 Ag2GeSe3 0.90 (Ag, Ge, Se) 32.0 47.0 15.0 38.000000 6.000000 34.0 65.0 89.0 24.0 79.333333 9.666667 89.0 72.6400 107.8682 35.2282 87.542733 13.550311 78.96000 494.00 1234.93 740.93 860.543333 366.543333 494.00 11.0 16.0 5.0 14.000000 2.000000 16.0 4.0 5.0 1.0 4.333333 0.444444 4.0 120.0 145.0 25.0 128.333333 11.111111 120.0 1.93 2.55 0.62 2.253333 0.296667 2.55 1.0 2.0 1.0 1.666667 0.444444 2.0 0.0 4.0 4.0 2.333333 1.666667 4.0 10.0 10.0 0.0 10.000000 0.000000 10.0 0.0 0.0 0.0 0.00000 0.000000 0.0 11.0 16.0 5.0 14.000000 2.000000 16.0 0.0 1.0 1.0 0.333333 0.444444 0.0 0.0 4.0 4.0 1.666667 1.111111 2.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 4.0 3.0 2.000000 0.666667 2.0 16.33 25.920000 9.590000 22.237500 3.938333 25.920000 0.0 0.799 0.799 0.463333 0.335667 0.799 0.0 0.0 0.0 0.0 0.0 0.0 14.0 225.0 211.0 119.500000 105.500000 14.0
4 Ag2HgI4 2.47 (Ag, Hg, I) 47.0 80.0 33.0 55.142857 7.102041 53.0 65.0 96.0 31.0 83.571429 14.204082 96.0 107.8682 200.5900 92.7218 131.992040 19.599417 126.90447 234.32 1234.93 1000.61 607.368571 358.606531 386.85 11.0 17.0 6.0 14.571429 2.775510 17.0 5.0 6.0 1.0 5.142857 0.244898 5.0 132.0 145.0 13.0 139.714286 3.020408 139.0 1.93 2.66 0.73 2.357143 0.346122 2.66 1.0 2.0 1.0 1.714286 0.408163 2.0 0.0 5.0 5.0 2.857143 2.448980 5.0 10.0 10.0 0.0 10.000000 0.000000 10.0 0.0 14.0 14.0 2.00000 3.428571 0.0 11.0 26.0 15.0 16.571429 3.183673 17.0 0.0 1.0 1.0 0.285714 0.408163 0.0 0.0 1.0 1.0 0.571429 0.489796 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 1.0 0.857143 0.244898 1.0 16.33 43.015000 26.685000 32.851084 11.615904 43.015000 0.0 1.062 1.062 0.606857 0.520163 1.062 0.0 0.0 0.0 0.0 0.0 0.0 64.0 225.0 161.0 124.571429 69.224490 64.0

Pause and reflect: Do you recognize any of the column headings? Why are we taking the average, min, max, etc. of the elemental features?

Remove correlated features

So far we’ve covered several best practices, such as scaling our input features for linear regression and performing cross validation to get a realistic assessment, and here we introduce one more. Whenever we’re working with more than one feature, there is a chance that a few of them will be very strongly [linearly] correlated. We’ve already discussed what the Pearson correlation coefficient (\(r\)) means, and the reason this is undesirable is because the correlation can influence feature importance and potentially cause numerical instabilities during fitting.

How can we spot these correlations and remove them from our dataset?

You already know the answer to the first part, which is by plotting a heatmap! Given a DataFrame, recall that we can compute the correlation between the columns using the df.corr() method. Then we can plot a pretty heatmap. 😊

bg_data_featurized = bg_data_featurized.dropna(how='any', axis=1)   # this removes columns w/ NaN
corr_matrix = bg_data_featurized.corr().abs()   # we take the absolute value
fig, ax = plt.subplots()
h = ax.imshow(corr_matrix)
plt.colorbar(h)
plt.show()
../../_images/features_blank_15_0.png

Cool! But maybe unlike the previous exercises where it was clear what each column and row represented, here there are just too many features involved. And so, this calls for an automated, programmatic approach, which is what the following code does. It removes the following columns:

  • For any two features that have a correlation \(|r| > 0.95\), it removes one of them.

  • Any of the columns with more than 100 0 values. This means the feature is 0 for > 95% of the data, and while it might not strictly speaking be necessary, we just won’t care about them here.

# get the upper triangular portion of correlation matrix, to avoid double counting/removing
upper_tri = corr_matrix.where(np.triu(np.ones(corr_matrix.shape), k=1).astype(bool))

# figure out which columns to drop
to_drop = [column for column in upper_tri.columns if any(upper_tri[column] > 0.95)]
to_drop += list(bg_data_featurized.columns[bg_data_featurized.isin([0]).sum() > 100])

# drop those columns
bg_data_cleaned = bg_data_featurized.drop(to_drop, axis=1)
display(bg_data_cleaned)
composition gap expt composition_pmg MagpieData minimum Number MagpieData maximum Number MagpieData range Number MagpieData mean Number MagpieData avg_dev Number MagpieData mode Number MagpieData minimum MendeleevNumber MagpieData maximum MendeleevNumber MagpieData mean MendeleevNumber MagpieData avg_dev MendeleevNumber MagpieData mode MendeleevNumber MagpieData minimum MeltingT MagpieData maximum MeltingT MagpieData range MeltingT MagpieData mean MeltingT MagpieData avg_dev MeltingT MagpieData mode MeltingT MagpieData maximum Column MagpieData mean Column MagpieData avg_dev Column MagpieData mode Column MagpieData maximum Row MagpieData range Row MagpieData avg_dev Row MagpieData minimum CovalentRadius MagpieData maximum CovalentRadius MagpieData range CovalentRadius MagpieData mean CovalentRadius MagpieData avg_dev CovalentRadius MagpieData mode CovalentRadius MagpieData minimum Electronegativity MagpieData maximum Electronegativity MagpieData range Electronegativity MagpieData mean Electronegativity MagpieData avg_dev Electronegativity MagpieData mode Electronegativity MagpieData minimum NsValence MagpieData maximum NsValence MagpieData mean NsValence MagpieData mode NsValence MagpieData maximum NpValence MagpieData range NpValence MagpieData mean NpValence MagpieData avg_dev NpValence MagpieData minimum NValence MagpieData maximum NValence MagpieData range NValence MagpieData mean NValence MagpieData avg_dev NValence MagpieData mode NValence MagpieData maximum NpUnfilled MagpieData range NpUnfilled MagpieData mean NpUnfilled MagpieData avg_dev NpUnfilled MagpieData maximum NUnfilled MagpieData mean NUnfilled MagpieData avg_dev NUnfilled MagpieData minimum GSvolume_pa MagpieData maximum GSvolume_pa MagpieData mean GSvolume_pa MagpieData avg_dev GSvolume_pa MagpieData mode GSvolume_pa MagpieData minimum SpaceGroupNumber MagpieData maximum SpaceGroupNumber MagpieData range SpaceGroupNumber MagpieData mean SpaceGroupNumber MagpieData avg_dev SpaceGroupNumber MagpieData mode SpaceGroupNumber
0 Ag0.5Ge1Pb1.75S4 1.83 (Ag, Ge, Pb, S) 16.0 82.0 66.0 36.275862 23.552913 16.0 65.0 88.0 83.482759 4.984542 88.0 388.36 1234.93 846.57 611.499655 251.480143 388.36 16.0 14.896552 1.217598 16.0 6.0 3.0 1.103448 105.0 146.0 41.0 119.724138 16.247325 105.0 1.93 2.58 0.65 2.396207 0.202806 2.58 1.0 2.0 1.931034 2.0 4.0 4.0 2.965517 1.141498 6.0 28.0 22.0 12.758621 7.700357 6.0 4.0 4.0 2.620690 1.046373 4.0 2.689655 0.994055 16.33000 28.110000 25.311724 1.875196 25.786875 70.0 225.0 155.0 139.482759 76.670630 70.0
1 Ag0.5Ge1Pb1.75Se4 1.51 (Ag, Ge, Pb, Se) 32.0 82.0 50.0 46.206897 17.388823 34.0 65.0 89.0 84.034483 5.479191 89.0 494.00 1234.93 740.93 669.783793 227.362568 494.00 16.0 14.896552 1.217598 16.0 6.0 2.0 0.760999 120.0 146.0 26.0 128.000000 11.034483 120.0 1.93 2.55 0.62 2.379655 0.187967 2.55 1.0 2.0 1.931034 2.0 4.0 4.0 2.965517 1.141498 11.0 28.0 17.0 18.275862 4.694411 16.0 4.0 4.0 2.620690 1.046373 4.0 2.689655 0.994055 16.33000 28.110000 25.385172 1.905589 25.920000 14.0 225.0 211.0 108.586207 104.370987 14.0
2 Ag2GeS3 1.98 (Ag, Ge, S) 16.0 47.0 31.0 29.000000 13.000000 16.0 65.0 88.0 78.833333 9.222222 88.0 388.36 1234.93 846.57 807.723333 419.363333 388.36 16.0 14.000000 2.000000 16.0 5.0 2.0 0.833333 105.0 145.0 40.0 120.833333 16.111111 105.0 1.93 2.58 0.65 2.268333 0.311667 2.58 1.0 2.0 1.666667 2.0 4.0 4.0 2.333333 1.666667 6.0 14.0 8.0 9.000000 3.000000 6.0 4.0 4.0 1.666667 1.111111 4.0 2.000000 0.666667 16.33000 25.786875 22.170937 3.893958 25.786875 70.0 225.0 155.0 147.500000 77.500000 70.0
3 Ag2GeSe3 0.90 (Ag, Ge, Se) 32.0 47.0 15.0 38.000000 6.000000 34.0 65.0 89.0 79.333333 9.666667 89.0 494.00 1234.93 740.93 860.543333 366.543333 494.00 16.0 14.000000 2.000000 16.0 5.0 1.0 0.444444 120.0 145.0 25.0 128.333333 11.111111 120.0 1.93 2.55 0.62 2.253333 0.296667 2.55 1.0 2.0 1.666667 2.0 4.0 4.0 2.333333 1.666667 11.0 16.0 5.0 14.000000 2.000000 16.0 4.0 4.0 1.666667 1.111111 4.0 2.000000 0.666667 16.33000 25.920000 22.237500 3.938333 25.920000 14.0 225.0 211.0 119.500000 105.500000 14.0
4 Ag2HgI4 2.47 (Ag, Hg, I) 47.0 80.0 33.0 55.142857 7.102041 53.0 65.0 96.0 83.571429 14.204082 96.0 234.32 1234.93 1000.61 607.368571 358.606531 386.85 17.0 14.571429 2.775510 17.0 6.0 1.0 0.244898 132.0 145.0 13.0 139.714286 3.020408 139.0 1.93 2.66 0.73 2.357143 0.346122 2.66 1.0 2.0 1.714286 2.0 5.0 5.0 2.857143 2.448980 11.0 26.0 15.0 16.571429 3.183673 17.0 1.0 1.0 0.571429 0.489796 1.0 0.857143 0.244898 16.33000 43.015000 32.851084 11.615904 43.015000 64.0 225.0 161.0 124.571429 69.224490 64.0
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
2149 ZrNiSb 0.55 (Zr, Ni, Sb) 28.0 51.0 23.0 39.666667 7.777778 28.0 44.0 85.0 63.333333 14.444444 44.0 903.78 2128.00 1224.22 1586.593333 455.208889 903.78 15.0 9.666667 3.777778 4.0 5.0 1.0 0.444444 124.0 175.0 51.0 146.000000 19.333333 124.0 1.33 2.05 0.72 1.763333 0.288889 1.33 2.0 2.0 2.000000 2.0 3.0 3.0 1.000000 1.333333 4.0 15.0 11.0 9.666667 3.777778 4.0 3.0 3.0 1.000000 1.333333 8.0 4.333333 2.444444 10.32000 31.560000 21.691667 7.581111 10.320000 166.0 225.0 59.0 195.000000 20.000000 166.0
2150 ZrO2 4.99 (Zr, O) 8.0 40.0 32.0 18.666667 14.222222 8.0 44.0 87.0 72.666667 19.111111 87.0 54.80 2128.00 2073.20 745.866667 921.422222 54.80 16.0 12.000000 5.333333 16.0 5.0 3.0 1.333333 66.0 175.0 109.0 102.333333 48.444444 66.0 1.33 3.44 2.11 2.736667 0.937778 3.44 2.0 2.0 2.000000 2.0 4.0 4.0 2.666667 1.777778 4.0 6.0 2.0 5.333333 0.888889 6.0 2.0 2.0 1.333333 0.888889 8.0 4.000000 2.666667 9.10500 23.195000 13.801667 6.262222 9.105000 12.0 194.0 182.0 72.666667 80.888889 12.0
2151 ZrS2 2.75 (Zr, S) 16.0 40.0 24.0 24.000000 10.666667 16.0 44.0 88.0 73.333333 19.555556 88.0 388.36 2128.00 1739.64 968.240000 773.173333 388.36 16.0 12.000000 5.333333 16.0 5.0 2.0 0.888889 105.0 175.0 70.0 128.333333 31.111111 105.0 1.33 2.58 1.25 2.163333 0.555556 2.58 2.0 2.0 2.000000 2.0 4.0 4.0 2.666667 1.777778 4.0 6.0 2.0 5.333333 0.888889 6.0 2.0 2.0 1.333333 0.888889 8.0 4.000000 2.666667 23.19500 25.786875 24.922917 1.151944 25.786875 70.0 194.0 124.0 111.333333 55.111111 70.0
2152 ZrSe2 2.00 (Zr, Se) 34.0 40.0 6.0 36.000000 2.666667 34.0 44.0 89.0 74.000000 20.000000 89.0 494.00 2128.00 1634.00 1038.666667 726.222222 494.00 16.0 12.000000 5.333333 16.0 5.0 1.0 0.444444 120.0 175.0 55.0 138.333333 24.444444 120.0 1.33 2.55 1.22 2.143333 0.542222 2.55 2.0 2.0 2.000000 2.0 4.0 4.0 2.666667 1.777778 4.0 16.0 12.0 12.000000 5.333333 16.0 2.0 2.0 1.333333 0.888889 8.0 4.000000 2.666667 23.19500 25.920000 25.011667 1.211111 25.920000 14.0 194.0 180.0 74.000000 80.000000 14.0
2153 ZrTaN3 1.72 (Zr, Ta, N) 7.0 73.0 66.0 26.800000 23.760000 7.0 44.0 82.0 67.600000 17.280000 82.0 63.05 3290.00 3226.95 1121.430000 1270.056000 63.05 15.0 10.800000 5.040000 15.0 6.0 4.0 1.680000 71.0 175.0 104.0 111.600000 48.720000 71.0 1.33 3.04 1.71 2.390000 0.780000 3.04 2.0 2.0 2.000000 2.0 3.0 3.0 1.800000 1.440000 4.0 19.0 15.0 7.600000 4.560000 5.0 3.0 3.0 1.800000 1.440000 8.0 4.800000 2.160000 14.76875 23.195000 17.124250 2.826600 14.768750 194.0 229.0 35.0 201.000000 11.200000 194.0

2154 rows × 71 columns

Finally, finally, finally build the ML model for CV

lr = LinearRegression()
kfold = KFold(n_splits=5, shuffle=True)
scaler = StandardScaler()

# only get the features (not the compositions, and certainly not the bandgap values!)
X = bg_data_cleaned.loc[:, featurizer.feature_labels()[0]:]
X_scaled = scaler.fit_transform(X)
y = bg_data_cleaned['gap expt']

# run cross validations AND store the predict values
yhat = cross_val_predict(lr, X_scaled, y, cv=kfold)

fig, ax = plt.subplots(figsize=(5,5))
ax.scatter(y, yhat, s=40)
ax.plot(y, y, c='k', zorder=-5)
ax.set_xlabel('actual band gap (eV)')
ax.set_ylabel('predicted band gap (eV)')
ax.set_xlim(-1, 13)
ax.set_ylim(-3, 13)
plt.show()
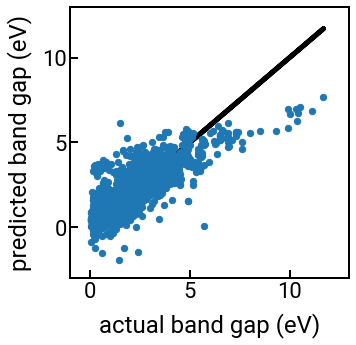
../../_images/features_blank_19_0.png
~ BREAK ~
At this point, we're going to give ourselves a short break before continuing further. Great work so far! 💪

Model complexity

Back to top

Wow, this featurization strategy is pretty cool, even if the new features can’t perfectly predict experimental band gaps. At least now we have an automated way to generate a bunch of physically-meaningful and interpretable features from the chemical formula, and it’s conceivable that we can add even more features from matminer or other packages/datasets, particularly if we account for the crystal structure.

But, if we continued in this way of blindly generating more and more features for ML, hoping to improve our model performance, then we’d actually fall for a trap! 🕳 Note that each time we add a feature, at least for linear regression, we also add a parameter (another coefficient) to the linear regression model. The addition of another parameter adds another degree of freedom that we must optimize for and increases the model complexity.

It is true that a more complex model should be able to learn more nuances in the data that it was trained on. Hence, a more complex model will generally have lower training error than a simpler model (fewer parameters). After all, physicist John von Neumann has famously said, “With four parameters I can fit an elephant, and with five I can make him wiggle his trunk.” 🐘

But what about unseen data, like the validation set in \(k\)-fold CV? If our model is a really complex polynomial and we have noisy or irregular data (always true in materials science), then it might not be a good approximation for new data, even when that data is an interpolation rather than extrapolation (where it would presumably do even worse). Thus at some point, the validation error will begin to increase with model complexity, even as the training error continues to decrease. At this point we say the model has started to overfit to the training data, and before this point, we might say the model is underfitting. At the point where validation error bottoms out is the Goldilocks sweet spot. 🐻

The code below illustrates this point by performing linear regression with increasingly complex polynomial features and plotting (a) the model on the left, and (b) the training and validation errors on the right. Note that we wrote several helper functions in a separate file to remove some of the clutter. For example, gen_data() is not some “well-known” function available everywhere; it was hard-coded for this example. Nonetheless, by revealing most of the important details, we hope to prove that we are not “gaming” anything.

from helper_funcs_04 import *

# generate some data
dom = np.reshape(np.linspace(0, 6, 1000), (-1, 1))
X_train, y_train, X_test, y_test = gen_data(dom)

# create plot objects and initial points on left side
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(17, 6))
ax[0].scatter(X_train, y_train, label='training pts')
ax[0].scatter(X_test, y_test, label='test pts')

# loop through increasingly complex models
train_errs, val_errs = [], []
degree = 8
for i in range(1, degree):

    # ML fitting helper function - return model and errors
    y_fit, train_err, val_err = ml_fitting(i, dom, X_train, y_train, X_test, y_test)
    train_errs.append(train_err)
    val_errs.append(val_err)
    
    # plot the low-degree polynomials for illustration on left side
    if i < 5:
        ax[0].plot(dom, y_fit, lw=3, label=f'degree {i}', c=f'C{i+1}')

# plots errors on the right and some nice styling
ax[1].plot(np.arange(1, degree), train_errs, label='training error')
ax[1].plot(np.arange(1 ,degree), val_errs, label='validation error')
plot_styling(ax, degree)
# fig.savefig('../../assets/fig/week_1/04/model_complexity.png')
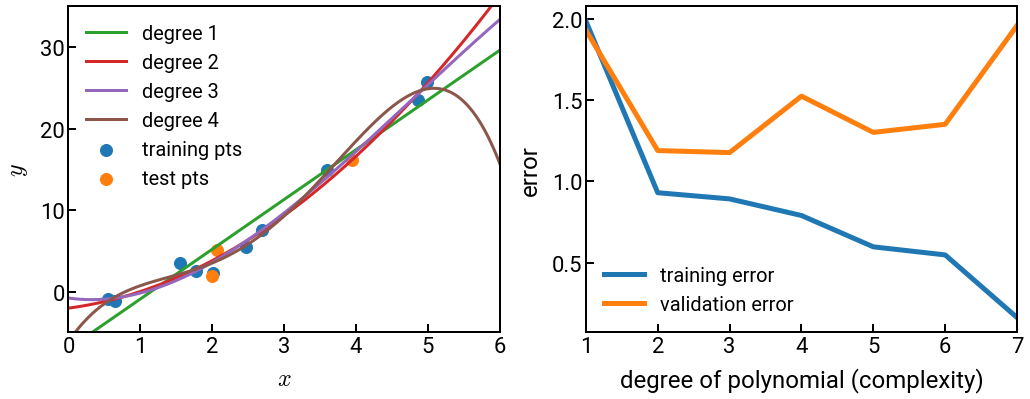
../../_images/features_blank_22_0.png

Feature selection

Back to top

While the previous example used a non-materials example, we hope you’ll believe us when we say that it happens with materials data too, more often than we would like. 😢 Therefore, we need a way to be able to perform feature selection after we have finished generating all of our features using matminer.

Once again, scikit-learn generously provides many built-in feature selection classes in the sklearn.feature_selection module. We’re going to go ahead and use a rather simple univariate feature selection tool called SelectKBest(score_func, k) that has the following parameters:

  • score_func: A scoring function callable that, for regression tasks, can either be f_regression or mutual_info_regression. These are functions imported from the sklearn.feature_selection module, and as callables we only need to write their name without parentheses to the function arguments.

  • k: An int for the number of top features to select.

Pause and reflect: How do we find the optimal value of k?

Exercise: apply feature selection to the band gap prediction problem and identify the top 10 features.

If you didn’t change anything, the featurized data should be stored in X.

Challenge: Can you then use only those 10 features to build a linear regression model? Does the model perform better or worse?

from sklearn.feature_selection import SelectKBest, f_regression, mutual_info_regression
selector = SelectKBest(score_func=f_regression, k=10)
selector_fitted = selector.fit(X, y)
selected_indices = selector_fitted.get_support(indices=False)
print(selected_indices)
# -------------   WRITE YOUR CODE IN THE SPACE BELOW   ---------- #

[ True False False  True False  True False False False False False False
 False False False False False False False False False False False False
  True False False  True False  True False  True  True False  True False
 False False False False False False False False False False False  True
 False False False False False False False False False False False False
 False False False False False False False False]

Conclusion

Congratulations on making it to the end! 🎉👏

There is a lot of information that we covered in this notebook, so it’s totally reasonable if not everything clicked right away and you find yourself needing to revist these concepts.

Please don’t hesitate to reach out on Slack if you have questions or concerns.

Featurization Advanced ML methods