More practice with ML models
Contents
More practice with ML models¶
Authors: Enze Chen and Mark Asta (University of California, Berkeley)
Note
This is an interactive exercise, so you will want to click the and open the notebook in DataHub (or Colab for non-UCB students).
Learning objectives¶
This notebook contains a series of exercises that will give you more practice building ML models in scikit-learn.
Contents¶
This notebook has the following sections.
Import Python packages¶
Please remember to run the following cell before continuing!
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.linear_model import LinearRegression, LogisticRegression
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, mean_absolute_error
from sklearn.model_selection import KFold, cross_val_score, cross_val_predict
from sklearn.metrics import confusion_matrix, accuracy_score
plt.rcParams.update({'figure.figsize':(8,6), # Increase figure size
'font.size':20, # Increase font size
'mathtext.fontset':'cm', # Change math font to Computer Modern
'mathtext.rm':'serif', # Documentation recommended follow-up
'lines.linewidth':5, # Thicker plot lines
'lines.markersize':12, # Larger plot points
'axes.linewidth':2, # Thicker axes lines (but not too thick)
'xtick.major.size':8, # Make the x-ticks longer (our plot is larger!)
'xtick.major.width':2, # Make the x-ticks wider
'ytick.major.size':8, # Ditto for y-ticks
'ytick.major.width':2, # Ditto for y-ticks
'xtick.direction':'in',
'ytick.direction':'in'})
Basic ML setup¶
Gather some data¶
This is always the first step.
For the sake of demonstration, let’s use the hardness-density dataset from the previous tutorials.
We will use the pandas package to help us load the data into a DataFrame, taking care to skip the first row.
hd = pd.read_csv('../../assets/data/hardness_density.csv', skiprows=1)
hd.head()
| Element | Number | Mohs hardness | Density (g/cc) | |
|---|---|---|---|---|
| 0 | lithium | 3 | 0.6 | 0.534 |
| 1 | beryllium | 4 | 5.5 | 1.850 |
| 2 | boron | 5 | 9.4 | 2.340 |
| 3 | carbon | 6 | 10.0 | 3.513 |
| 4 | sodium | 11 | 0.5 | 0.968 |
Exercise: Construct a linear model that predicts the Mohs hardness using the atomic number¶
You can use the entire dataset as the training set and the test set. Don’t forget to compute an error (in this case, training error) to assess model performance!
X = hd[['Number']]
y = hd['Mohs hardness']
# ------------- WRITE YOUR CODE IN THE SPACE BELOW ---------- #
Exercise: Now compare the ratio of the RMSE to the GTME¶
Is your model a good model? Is this what you would expect?
# ------------- WRITE YOUR CODE IN THE SPACE BELOW ---------- #
Exercise: Repeat the previous two steps, but now use the density AND atomic number¶
# ------------- WRITE YOUR CODE IN THE SPACE BELOW ---------- #
Exercise: Construct a parity plot of these new results¶
This will allow you to see which materials the model is performing poorly on.
# ------------- WRITE YOUR CODE IN THE SPACE BELOW ---------- #
Use a ML model for screening¶
So far, we haven’t explicitly shown you how a ML model can be used for screening purposes to search for materials with good properties. Let’s do that now, first with a picture that we’ve already shown:
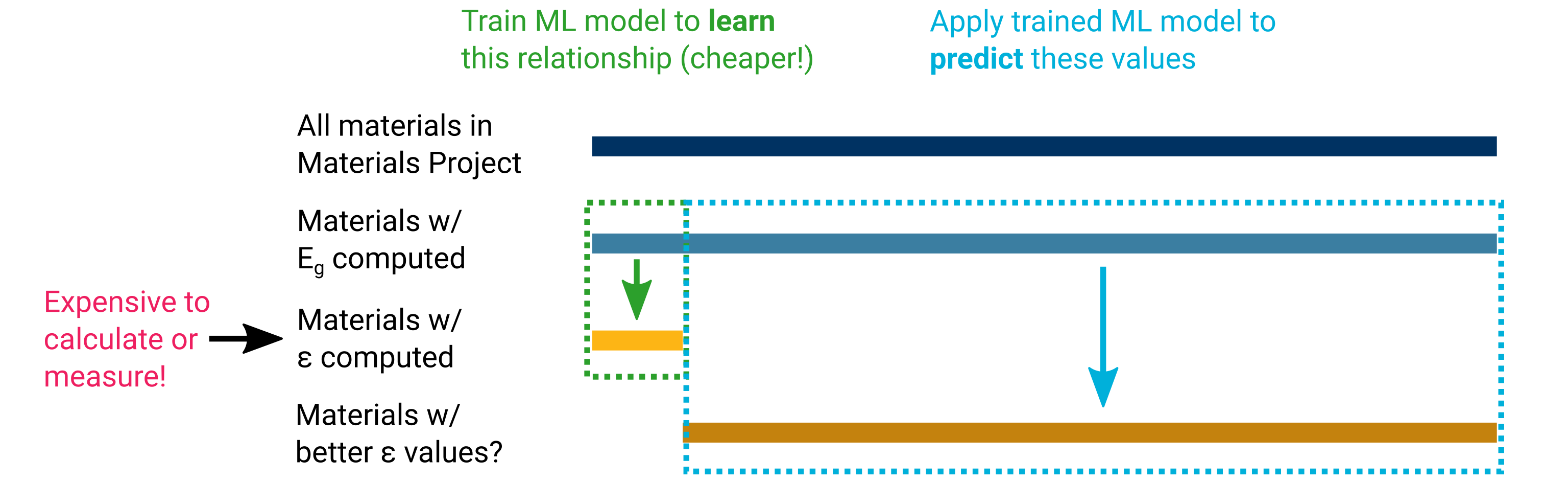
The first step is to establish a model between a commonly-available material property and the dielectric constant. For the sake of demonstration, we’ll choose the band gap and use the existing dataset supplied by the Petousis paper.
diel = pd.read_csv('../../assets/data/dielectric_dataset.csv')
diel.head()
| mp-id | formula | n | band_gap | diel_total | diel_elec | |
|---|---|---|---|---|---|---|
| 0 | mp-441 | Rb2Te | 1.86 | 1.88 | 6.23 | 3.44 |
| 1 | mp-22881 | CdCl2 | 1.78 | 3.52 | 6.73 | 3.16 |
| 2 | mp-28013 | MnI2 | 2.23 | 1.17 | 10.64 | 4.97 |
| 3 | mp-567290 | LaN | 2.65 | 1.12 | 17.99 | 7.04 |
| 4 | mp-560902 | MnF2 | 1.53 | 2.87 | 7.12 | 2.35 |
Exercise: Using the dataset above, train an ML model that maps \(E_{\mathrm{g}}\) to \(\varepsilon\)¶
But unlike before, don’t make any predictions yet!
# ------------- WRITE YOUR CODE IN THE SPACE BELOW ---------- #
Exercise: Now gather some more data without values of \(\varepsilon\)¶
You should be able to do this yourself now! Think about what criteria are important here. Start small.
We’ve also scraped a subset of the Materials Project and saved it in the more_mp_materials.csv file.
However, this dataset contains all types of materials, including metals, which could be misleading.
If you use this dataset, be sure to filter those out first.
# ------------- WRITE YOUR CODE IN THE SPACE BELOW ---------- #
Exercise: Make some predictions with the trained model¶
# ------------- WRITE YOUR CODE IN THE SPACE BELOW ---------- #
Challenge¶
But now without a ground truth to compare to, we can’t really calculate an error or make a parity plot. How can we make sense of our predictions, and whether our model is believable? Is this model any good? 🧐
More practice¶
Exercise: You can use the dataset of elemental properties and do some more modeling of your choosing¶
The file is elem_props.csv located in the same place as the other data.
Try to do one regression problem and one classification problem!
Also, instead of evaluating training error, do \(k\)-fold CV!
Hints:
After loading the data in, you want to narrow down a subset of columns first, comprising inputs and outputs.
From your subset DataFrame, you may have to remove rows with
NaNvalues.
# ------------- WRITE YOUR CODE IN THE SPACE BELOW ---------- #