Forced vibrations - Your turn

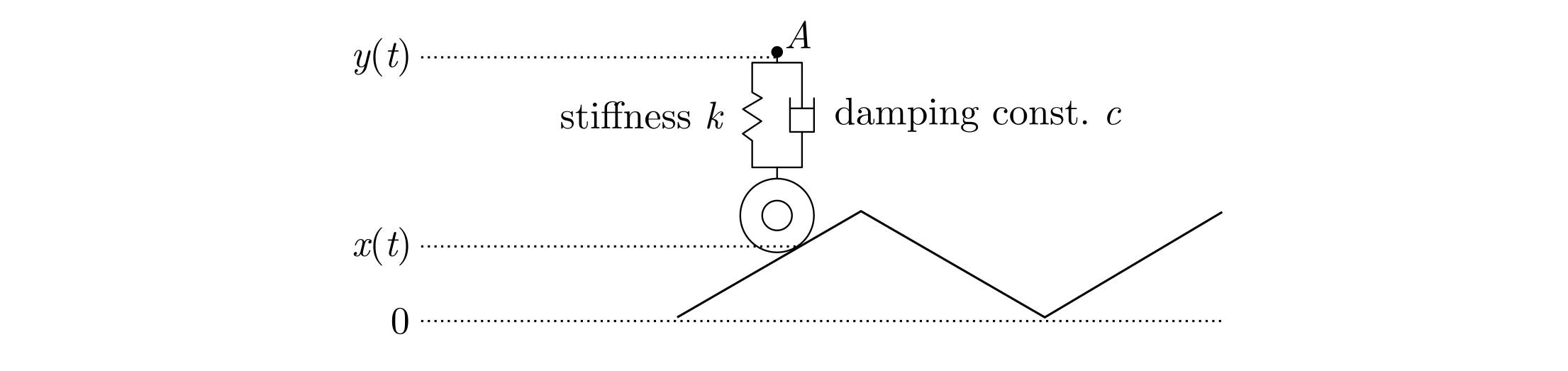
Forced vibrations - Your turn#

vibrations

You’re in your car driving on a rough road. Suppose that the shape of the road is given by the equation:

\[\begin{split} x(t) = \begin{cases} \dfrac{t}{T} - \dfrac{1}{2} & 0 < t < T \\ -\dfrac{t}{T} - \dfrac{1}{2} & T < t < 2T \end{cases} \end{split}\]

The mass of the car is \(m = 1.5 \times 10^3\) kg.

Newton’s law applied to the point above the suspension gives:

\[ m \dfrac{d^2y}{dt^2} = -k(y - x) - c \left( \dfrac{dy}{dt} - \dfrac{dx}{dt} \right) \tag{1} \]

with

  • \(y(t)\) the displacement of the point \(A\).

  • \(x(t)\) the shape of the road.

Equation 1 can be rewritten as:

\[ m \dfrac{d^2y}{dt^2} + c \dfrac{dy}{dt} + ky = kx + c \dfrac{dx}{dt} \]

Assuming the solution of the form \(y(t) = \sum_{n=1}^{\infty} A_n \cos(n \pi t) + B_n \sin (n \pi t)\), we obtain the following Fourier series representation for \(y\):

\[ y(t) = \sum_{n\ \text{odd}} A_n \cos \left( \dfrac{n\pi t}{T} \right) + B_n \sin \left( \dfrac{n\pi t}{T} \right) \]

with \(A_n = \dfrac{C_2 C_3 - C_1 C_4}{C_1^2 + C_2^2}\) and \(B_n = \dfrac{C_3 - C_2 A_n}{C_1}\), where

\[ C_1 = \dfrac{c \pi n}{T}, \quad C_2 = k - \dfrac{m \pi^2 n^2}{T^2}, \quad C_3 = -\dfrac{4k}{n^2\pi^2}, \quad C_4 = \dfrac{4c}{n \pi T} \]

Part (a)#

Using the equations above, write a code which computes the displacement of point \(A\). Test your code with the following cases: \(T = 5\) s, \(\Delta t = 0.05\) s.

Case

Stiffness \(k\) (m/s²)

Damping constant \(c\) (m/s)

1

\(10^4\)

\(100\)

2

\(10^5\)

\(100\)

3

\(10^6\)

\(100\)

4

\(10^5\)

\(10\)

5

\(10^5\)

\(1000\)

In each case, plot the vertical displacement as a function of time for \(t\) between \(0\) and \(4T\) and the contribution of each frequency to the displacement using the ax.stem() command.

# TODO: Write your solution below

Part (b)#

What are the effects of \(k\) and \(c\) on the displacement of point \(A\)?

TODO: Write your answer in the space below#

Exporting your work#

When you’re ready, the easiest way to export the notebook is to File > Print it and save it as a PDF. Remove any excessively long, unrelated outputs first by clicking the arrow → next to the output box and then Show/hide output. Obviously don’t obscure any necessary output or graphs!

Contents