Contents

MSE 104L laboratory 1 exercises

MSE 104L laboratory 1 exercises

Authors: Enze Chen (University of California, Berkeley)

Note

This is an interactive exercise, so you will want to click the and open the notebook in DataHub (or Colab for non-UCB students).

This notebook contains a series of exercises to help you process your data from Lab 1. It doesn’t answer all of the discussion questions in the lab procedures, but it will help you create a series of figures that can structure the narrative of your lab report. We hope it makes the writeup easier!

We tried to stagger the guidance such that each exercise only introduces a few new ideas at a time. These new ideas are marked with a ⭐.
We understand that many students' plots may now look very similar, but please make sure to write your own code and lab reports. That will lead to deeper learning.

Import Python packages

It can be pretty helpful to import all required packages at the top of the notebook, which we’ve done below. Please modify the settings as needed. Run the cell below using Shift+Enter.

# You can import other packages if you want, but you shouldn't have to.
import numpy as np
import matplotlib.pyplot as plt

plt.rcParams.update({
    'figure.figsize': (5,4),   # You might want to change this to be wider for spectra!! 
    'font.size':         18,
    'lines.linewidth':  2.5,
    'lines.markersize':  10,
    'axes.linewidth':     2,
    'xtick.major.size':   8,
    'xtick.major.width':  2,
    'ytick.major.size':   8,
    'ytick.major.width':  2
})

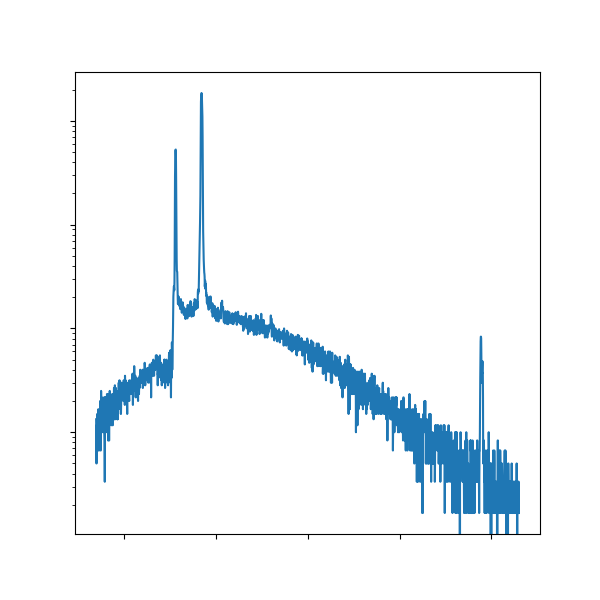
Visualizing an emission spectra

Back to top

Since you went through all that trouble to gather a Cu emission spectra experimentally, let’s now plot it! When talking about any kind of scientific phenomenon, it’s often helpful to include a representative figure. 😉

  1. First, you’ll want to upload the diffractometer data to the folder containing this notebook in JupyterHub (📁 > mse104l > lab1).

  2. Then you can load the data into a NumPy array with np.loadtxt().

  3. ⭐ Then plot it with Matplotlib! (ax.plot())

  4. ❗Don’t forget styling elements! Here’s the character for theta: θ

  5. Download the saved figure and paste it into your lab writeup. You can find the saved figure in the same JupyterHub directory as above.

# -------------   WRITE YOUR CODE IN THE SPACE BELOW   ---------- #
bare_data = 'my_Cu_file.txt'   # replace this with your file name

Cu_bare = np.loadtxt(bare_data, delimiter=',')

fig, ax = plt.subplots()   # create and style a plot below

plt.show()
fig.savefig('Cu_bare.png', dpi=300, bbox_inches='tight')

Some thoughts on styling

From our experience:

  • It is almost always the case that your fonts (e.g., labels) and line thickness need to be larger than you expect. This is because the figure will be shrunk in your report/poster/etc., but it still needs to be readable.

  • Titles are somewhat optional, as they just take up valuable space from your data. Throw the descriptions into your figure captions in your report.

  • Intensities are somewhat arbitrary, so you can give it units of (a.u.) and omit the bulky \(y\)-ticks/labels by passing yticks=[] to ax.set(). More space for your data!

Multiple spectra - different filter elements

Back to top

Part of the lab asks you to identify the absorption edges of different metal elements used in the filters. You could just inspect each spectra individually, but it might be more compelling if you compared 1-vs-1 with the bare Cu spectra. If you want to plot multiple curves on the same axis:

  1. Copy the code from above and add another ax.plot() call to add a second spectra featuring one of the elemental filters.

    • ⭐ We recommend adding labels and a legend to help distinguish them.

    • ⭐ We recommend making the colors for each elemental filter consistent. You can choose the color name from these lists and set it using the c parameter: ax.plot(x, y, c='my_color_name').

    • We do not recommend plotting all filters onto the same plot.

  2. ⭐ To help reveal the absorption edge, we recommend changing the scale on the \(y\)-axis. You can do so by passing yscale='value', to the ax.set() method, where value is chosen from here.

# -------------   WRITE YOUR CODE IN THE SPACE BELOW   ---------- #

Multiple spectra - different filter thicknesses

Back to top

Another part of the lab asks you to observe how the absorption spectra changes with respect to Ni filters of different thicknesses. There are two plots that are helpful here.

You might want to consider a plot with the bare Cu spectra and the four different Ni spectra on the same plot. This allows you to see how the filters progressively change the intensity.

  • ⭐ To zoom in on the region (peak) of interest, you can change the \(x\)-axis limits with a xlim=(start,end) argument in the ax.set() method. You have to figure out the appropriate limits to capture the interesting behavior.

  • ⭐ Make sure you clearly label all of your plots and include a legend. It’s handy that Matplotlib automatically cycles through different colors.

  • You may want to reset some of your Pyplot settings, depending on what you had set previously. You can begin the cell below with another plt.rcParams.update() call and just update figure.figsize and font.size.

# -------------   WRITE YOUR CODE IN THE SPACE BELOW   ---------- #
plt.rcParams.update({})   # add key:value pairs here

Scatterplot and curve fitting

Back to top

The second plot is regarding the mass absorption coefficient, \(\mu/\rho\), given by the equation:

\[ I_x = I_0 \exp \left[ -\left( \frac{\mu}{\rho} \right) \rho x \right] \]

where \(I_0\) and \(I_x\) are the incident and transmitted intensities, respectively, \(\rho\) is the density, and \(x\) is the distance traveled through the absorbing medium. You have collected the values of \(I_0\) and \(I_x\), you’ve been told \(x\), and you can look up tabulated values of \(\rho\). The individual points will have noise, so it’s best to compute a line of best fit and then extract the mass absorption coefficient \(\mu/\rho\).

Here are some more hints:

  • You should probably manually create NumPy arrays for your values with the syntax: x=np.array(list_of_values) and similarly for y.

  • ⭐ To take the natural logarithm of an array, use np.log(arr).

  • ⭐ To calculate a line of best fit in Python, you can use the np.polyfit(x, y, degree) command as follows:

c = np.polyfit(x, y, 1)

where x and y hold your values and 1 specifies a degree 1 polynomial (line). The resulting coefficients are stored in the c array in decreasing order of \(x\); that is, \(c = [c_0, c_1, \dots, c_n]\) where \(c_0 x^n + c_1 x^{n-1} + \cdots + c_{n-1} x + c_n \) for a degree \(n\) polynomial fit.

  • ⭐ Just as ax.plot() is for curves, ax.scatter(x, y) can be used for individual points.

# -------------   WRITE YOUR CODE IN THE SPACE BELOW   ---------- #

Conclusion

Back to top

This concludes the plotting exercises for Lab 1. Congratulations! We hope you’re proud of the plots that you generated and we wish you luck with the lab writeup. 📝

Note that the plot for Moseley’s relation, while not discussed explicitly here, follows the last exercise closely.

previous

Introduction to data visualization in Python

next

Lab 2: Powder X-ray Diffraction