1. Random number generation

Important!

If you’re completely new to Python, you may want to go through the exercises in the Python fundamentals notebook first!

There are many instances in probability and statistics, particularly when it comes to sampling, that you will need to produce random numbers or simulate random processes. This can be done quite efficiently in Python, allowing you to model engineering designs with greater confidence.

Note

The syntax for generating random numbers in Python has evolved over the years, so this workbook tries to follow current best practices!

Summary of commands

In this exercise, we will demonstrate the following:

• Numpy

  • np.random.default_rng() - Object for generating random values.

    • Optional seed for consistent values.

  • rng.uniform(low, high, size) - Generates a random array of size dimensions from a uniform distribution between [low, high).

    • If size is not specified, then a single value is generated.

  • np.abs(arr) - Takes the absolute value of all elements in arr.

  • np.sum(arr) - Sums the values in arr.

    • Can be along a specific axis if given.

• Matplotlib

  • plt.subplots() - Create Figure and Axes objects for plotting. Many optional parameters.

  • ax.hist(arr, bins) - Create a frequency plot (histogram) of the elements in arr, grouped into bins columns if specified (otherwise auto-calculated).

Demo

We will attempt to solve one of the homework problems numerically by performing a virtual experiment using NumPy’s random number generator. The problem is as follows:

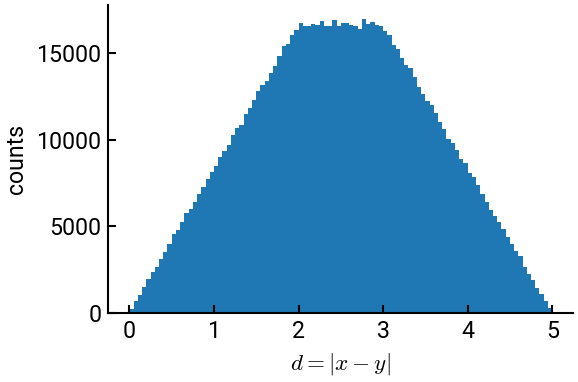
Two points \(a\) and \(b\) are selected at random along the \(x\)-axis such that \(-2 \le b \le 0\) and \(0 \le a \le 3\). Find the probability that the distance between \(a\) and \(b\) is greater than \(3\) by performing one million trials. Make a histogram of the generated distances between \(a\) and \(b\).

Hint: Generating a vector of random numbers all at once is computationally more efficient than generating random values one at a time within a for loop!

# import necessary libraries
import numpy as np

# create the rng object; we use a seed for consistent results
rng = np.random.default_rng(seed=1)

# store the number of trials
N = int(1e6)

# draw the samples and compute the values
b = rng.uniform(-2, 0, N)
a = rng.uniform(0, 3, N)
d = np.abs(a - b)
s = np.sum(d > 3)    # inner argument creates a logical array/mask of 0/1
print(f"Probability = {s/N:.3f}")

Probability = 0.333

The final line uses the special f-strings construct, which we encourage you to learn as it’s very efficient.

Now that we have the data, we can also plot it.

# import necessary libraries
import matplotlib.pyplot as plt

# create the Figure and Axes objects
fig, ax = plt.subplots()

# make the histogram 
ax.hist(d, bins=100)

# style the plot (with LaTeX!) and show it
ax.set(xlabel=r"$d = |x - y|$", ylabel='counts')
plt.show()